Data exploration

Data exploration

1. Outliers Y & X

• Outliers in response variable vs in covariates - to be dealt with differently
• Transformation less desirable for response variable than in covariates?

2. Homogeneity Y

3. Normality Y

• Example of importance of biological intuition and graphical investigation
  • Fig 5b - transformation to get normality not desirable

4. Zero troble Y

• Zero-inflated GLM
• Double zeros, or joint absences - what do they mean? e.g., spatial clumping
• Multivariate analysis that ignores double zeros

5. Collinearity X

• VIF of 10, 3, or 2 - reason for these values?
• VIFs, or common sense or biological knowledge

6. Relationships Y & X

• Multi-panel scatter plots for checking for outliers

7. Interactions

• Are data balanced? Use coplot (Fig 11).

8. Independence Y

• Mixed effects, etc. to deal with non-independence
• ACF or variograms for checking for temporal and spatial non-independence

Not all steps always needed

Common themes

• Biological intuition = key to make decisions about stats
• Hypothesis testing vs hypothesis generation
  • One solution - two data sets - one to create hypotheses and one to test them
  • But only practical for large data sets
• Emphasis on graphical tools

Checking for outliers

Zurr et al. recommends plotting your data using boxplots and dotcharts to detect outliers. Before removing suspected outliers, make sure they are actually outliers!

Since my data is multivariate, I used sequence count per sample for outlier detection in the following examples.

Boxplot

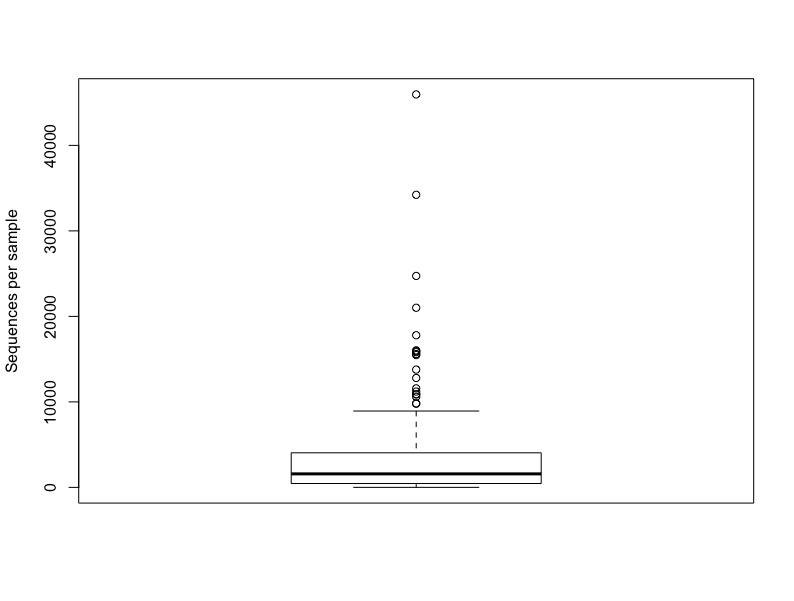
boxplot(sample_sums(merged_data),  ylab = "Sequences per sample")

Cleveland dotchart

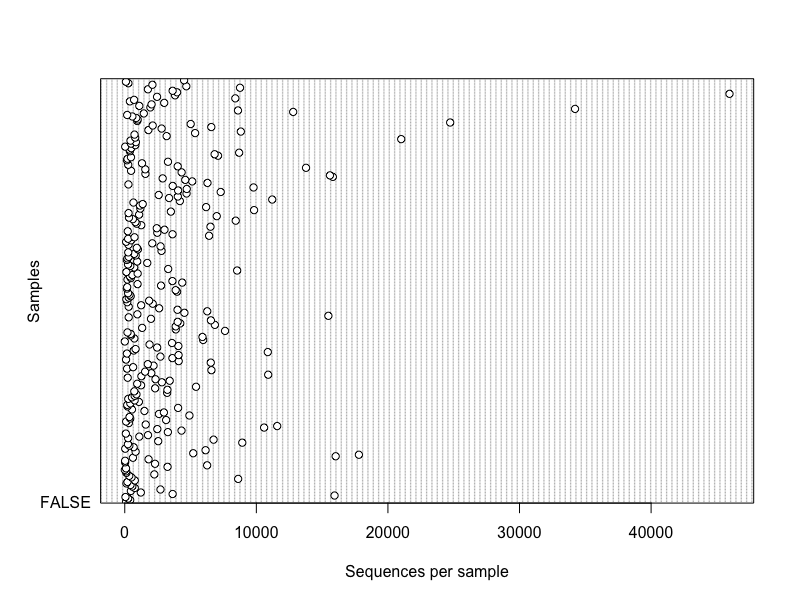
dotchart(sample_sums(merged_data), xlab = "Sequences per sample",
         ylab = "Samples", labels = F)

Plotly - great visualization tool

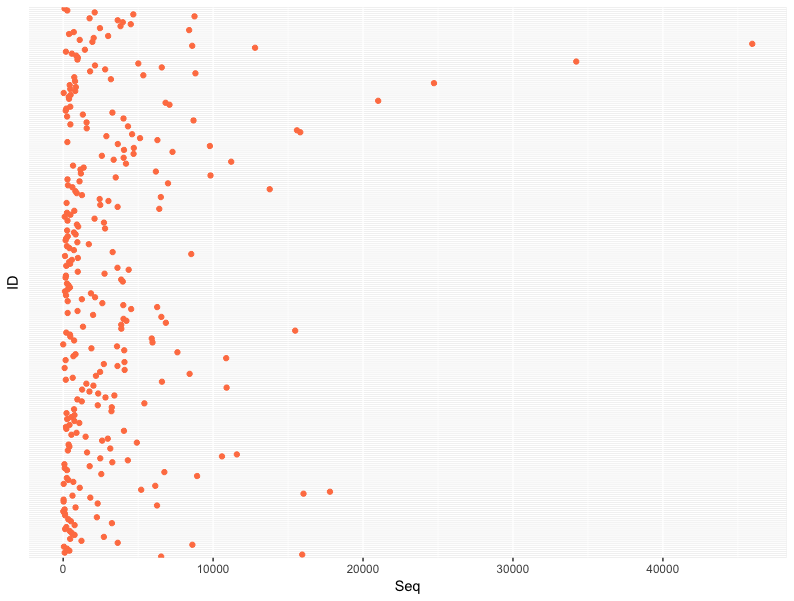
seq_num <- data.frame(ID=sample_data(merged_data)$ID, Seq=sample_sums(merged_data))
dot_gg <- ggplot(seq_num, aes(x=Seq,y=ID)) + geom_point(col="coral") + 
  theme(axis.text.y = element_blank(), axis.ticks.y = element_blank())
ggplotly(dot_gg)

Dotchart for multiple variables

Since most of the variables in my dataset are categorical, here I used raw data (sequence count) subsetted by bird species.

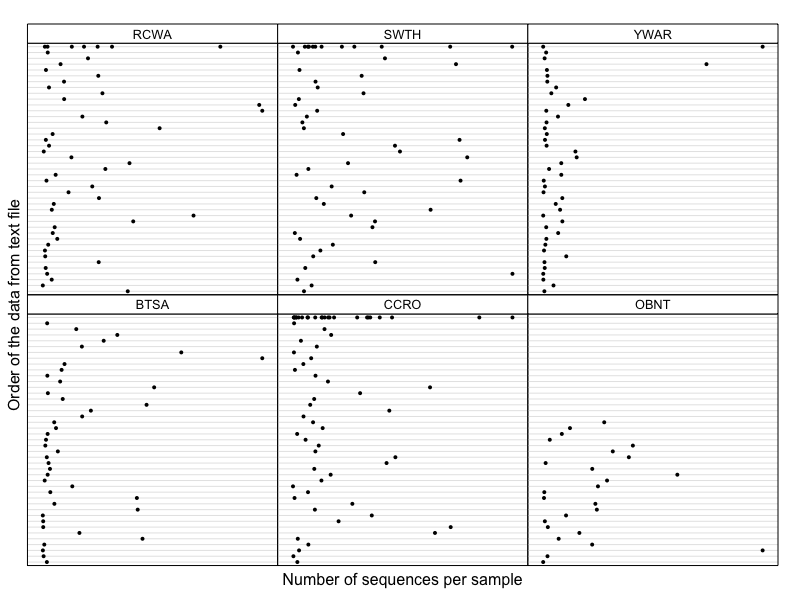
Z <- qpcR:::cbind.na(sample_sums(data.BTSA), sample_sums(data.CCRO), sample_sums(data.OBNT),
           sample_sums(data.RCWA), sample_sums(data.SWTH), sample_sums(data.YWAR))
colnames(Z) <- c("BTSA", "CCRO", "OBNT", "RCWA", "SWTH", "YWAR")
dotplot(as.matrix(Z), groups = FALSE,
        strip = strip.custom(bg = 'white',
        par.strip.text = list(cex = 0.8)),
        scales = list(x = list(relation = "free"),
                      y = list(relation = "free"),
                      draw = FALSE),
        col = 1, cex  = 0.5, pch = 16,
        xlab = "Number of sequences per sample",
        ylab = "Order of the data from text file")

Your data’s distribution

Some statistical tests assume normal distributions, making it important to check the shape of your data. Plot a histogram with all of your data and then groups of your data.

“If you want to apply a statistical test to determine whether there is significant group separation in a discriminant analysis, however, normality of observations of a particular variable within each group is important”

Histogram

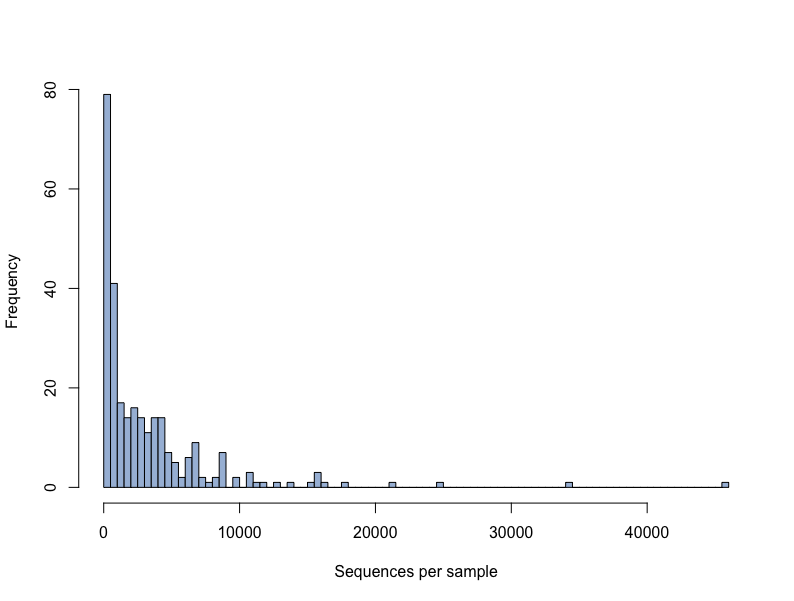
hist(sample_sums(merged_data), breaks = 100,col = "#a6bddb", xlab="Sequences per sample", main = ' ')